Semi-parametric SIR
Author: Erik M Volz @emvolz
Date: 2018-10-02
R implementation of SDEs using the pomp library and Euler-Murayama algorithm.
library(pomp)
set.seed( 1111 )
# Function to simulate one time step
step_fun_R <- function(x, t, params, delta.t, ...){
S <- x[1]
I <- x[2]
R <- x[3]
N <- S + I + R
logbeta <- x[4]
beta <- exp(logbeta)
gamma = params[1]
sigma = params[2]
alpha = params[3]
newinf <- beta * S * I * delta.t/N
newdeath <- gamma * I *delta.t
S <- max(0, S - newinf )
I <- max(0, I + newinf - newdeath )
R <- max(0, R + newdeath )
logbeta <- logbeta + rnorm(1, -alpha * I * delta.t, sd = sigma * sqrt(delta.t) )
c( S = unname(S) , I = unname(I), R = unname(R), logbeta = unname( logbeta ))
}
# Defines pomp object that could be used for simulation or inference
spsir_pomp_R <- pomp ( rprocess = euler.sim( step.fun = step_fun_R, delta.t = .001)
, t0 = 0
, statenames = c( 'S', 'I', 'R', 'logbeta')
, paramnames = c('gamma', 'sigma', 'alpha')
, data = data.frame( time = seq(0, 10, by=.01), S = NA, I = NA, R = NA, logbeta = NA)
, time = 'time'
, initializer = function(params, t0, ... ) c( S = 50, I = 1, R = 0, logbeta = log(3) )
, rmeasure = function( x, t, params, ... ) x
)
Simulation
spsir_pomp_R_sol <- simulate(spsir_pomp_R, params = c( gamma = 1, sigma = 1, alpha = 0.1) )
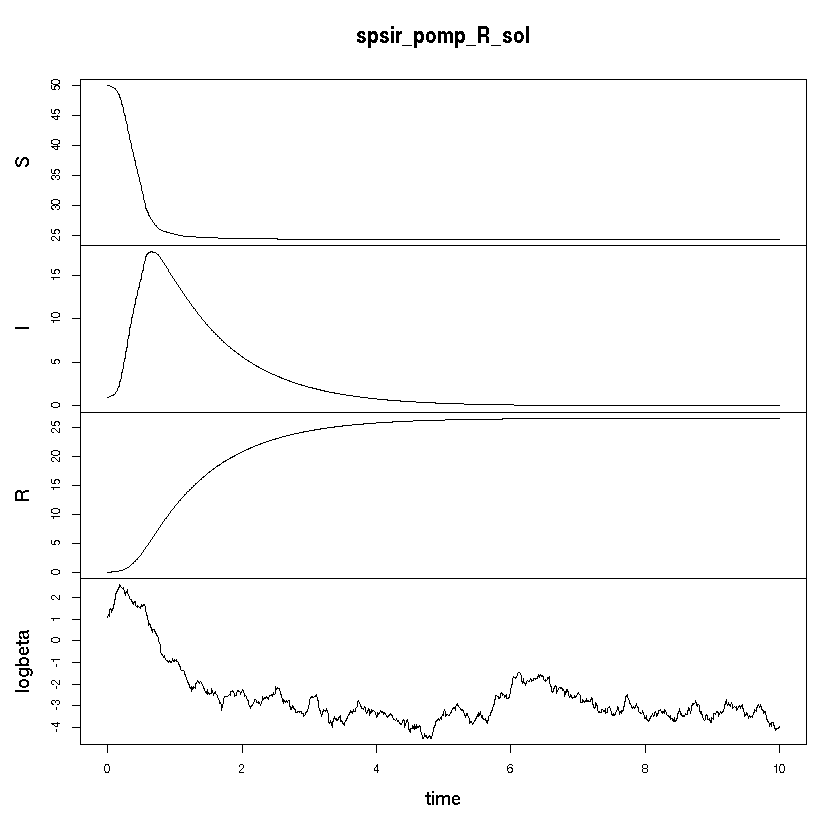
Visualization
plot( spsir_pomp_R_sol )