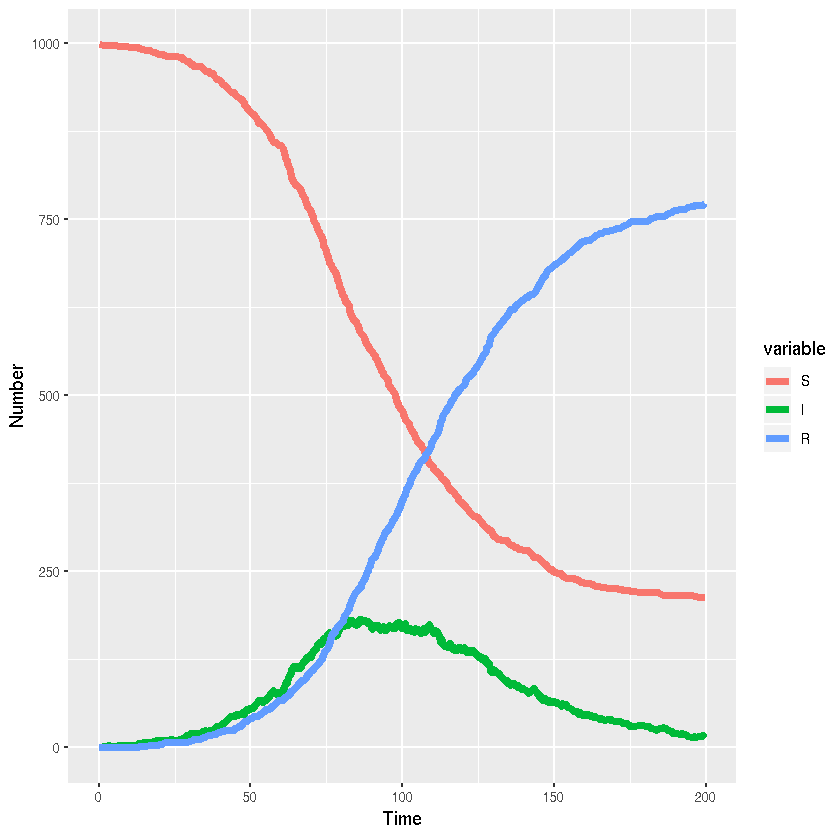
Stochastic SIR model (discrete state, continuous time) in R/Rcpp
library(reshape2)
library(Rcpp)
cppFunction('
List sirc(double beta, double gamma, double N, double S0, double I0, double R0, double tf){
double t = 0;
double S = S0;
double I = I0;
double R = R0;
std::vector<double> ta;
std::vector<double> Sa;
std::vector<double> Ia;
std::vector<double> Ra;
do{
ta.push_back(t);
Sa.push_back(S);
Ia.push_back(I);
Ra.push_back(R);
double pf1 = beta*S*I;
double pf2 = gamma*I;
double pf = pf1+pf2;
double dt = rexp(1,pf)[0];
t += dt;
double r = runif(1)[0];
if(r<pf1/pf){
S--;
I++;
}else{
I--;
R++;
}
if(I==0){break;}
} while (t<=tf && (I>0));
return List::create(_["time"] = ta, _["S"] = Sa, _["I"] = Ia, _["R"]=Ra);
}'
)
set.seed(42)
sir_out_list <- sirc(0.1/1000,0.05,1000,999,1,0,200)
sir_out <- as.data.frame(sir_out_list)
if(dim(sir_out)[1]==1){
sir_out_list <- sirc(0.1/1000,0.05,1000,999,1,0,200)
sir_out <- as.data.frame(sir_out_list)
}
head(sir_out)
| 0.000000 | 999 | 1 | 0 |
| 1.891201 | 998 | 2 | 0 |
| 3.470562 | 997 | 3 | 0 |
| 4.169704 | 997 | 2 | 1 |
| 8.149657 | 996 | 3 | 1 |
| 11.145904 | 995 | 4 | 1 |
sir_out_long <- melt(sir_out,"time")
Visualisation
library(ggplot2)
ggplot(sir_out_long,aes(x=time,y=value,colour=variable,group=variable))+
# Add line
geom_line(lwd=2)+
#Add labels
xlab("Time")+ylab("Number")